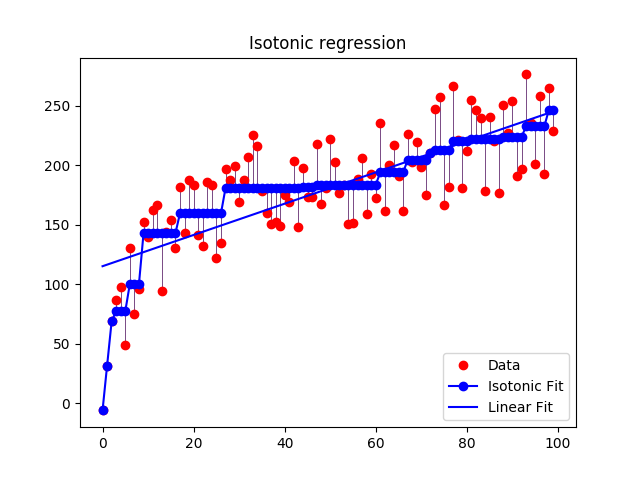
1.15. Isotonic regression¶

The class IsotonicRegression fits a non-decreasing function to data. It solves the following problem:

minimize $\sum_{i} w_{i} (y_{i} - {\hat{y}}_{i})^{2}$

subject to ${\hat{y}}_{m i n} = {\hat{y}}_{1} \leq {\hat{y}}_{2} . . . \leq {\hat{y}}_{n} = {\hat{y}}_{m a x}$

where each $w_{i}$ is strictly positive and each $y_{i}$ is an arbitrary real number. It yields the vector which is composed of non-decreasing elements the closest in terms of mean squared error. In practice this list of elements forms a function that is piecewise linear.

../_images/sphx_glr_plot_isotonic_regression_0011.png