Note
Click here to download the full example code or run this example in your browser via Binder
Illustration of prior and posterior Gaussian process for different kernels¶
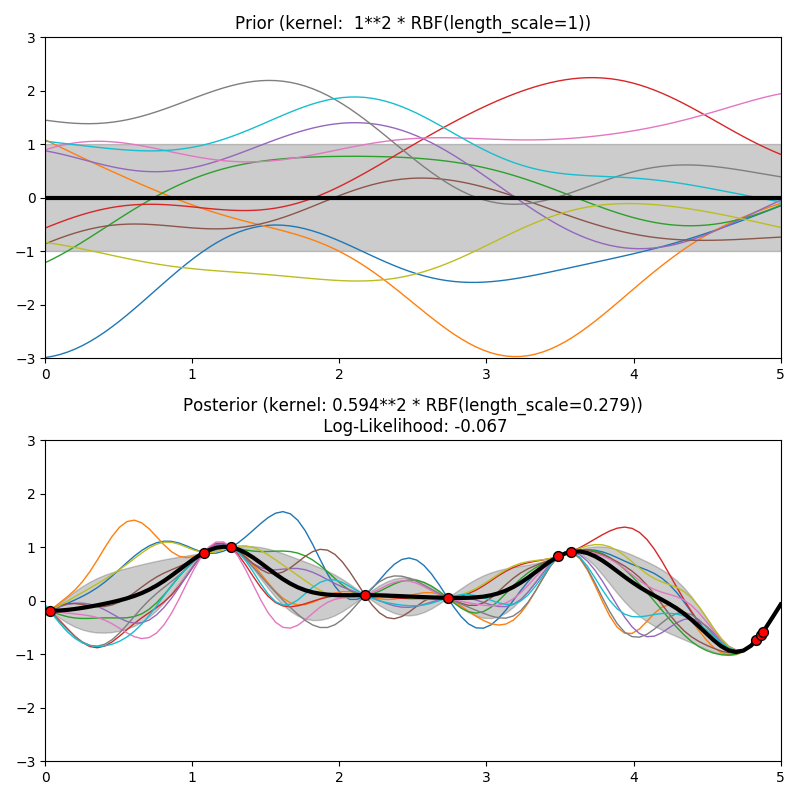
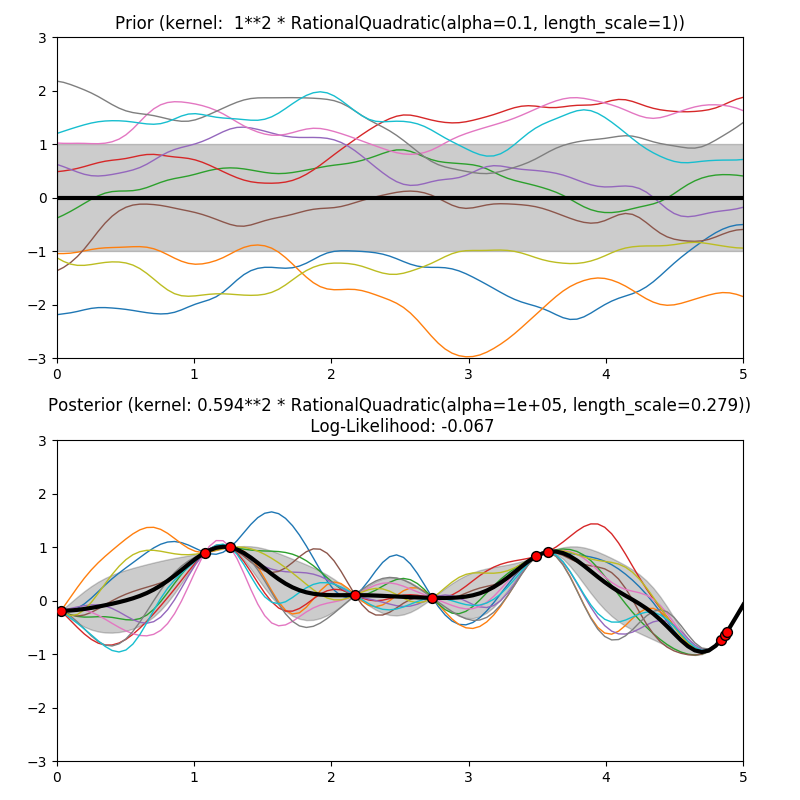
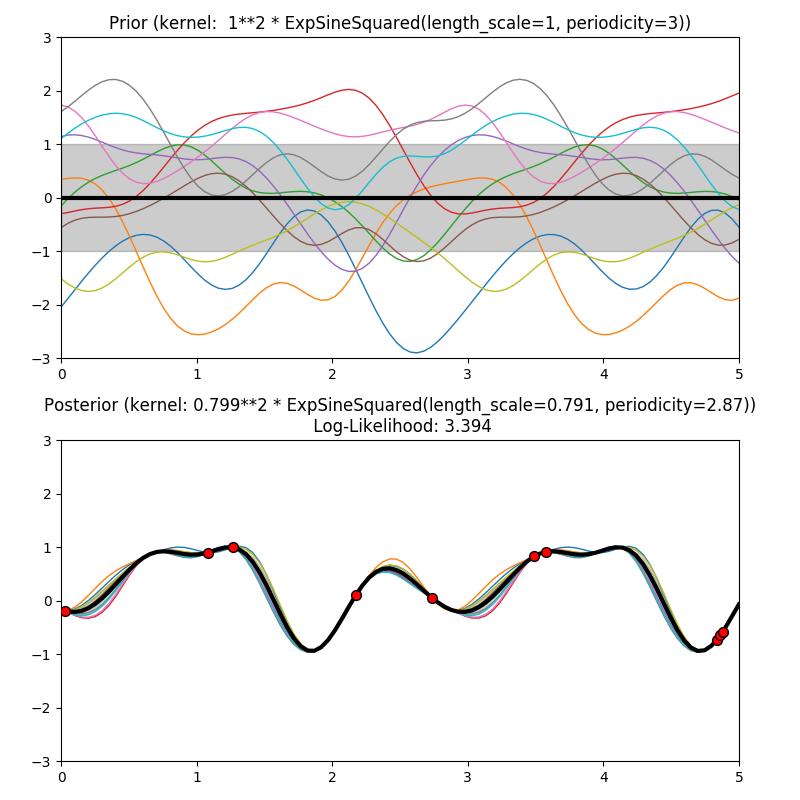
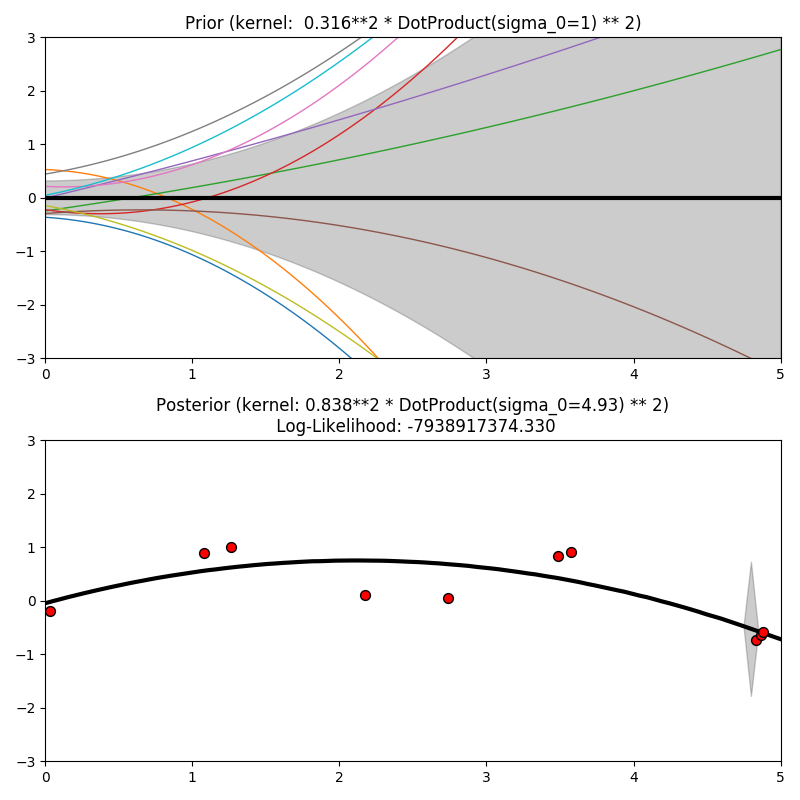
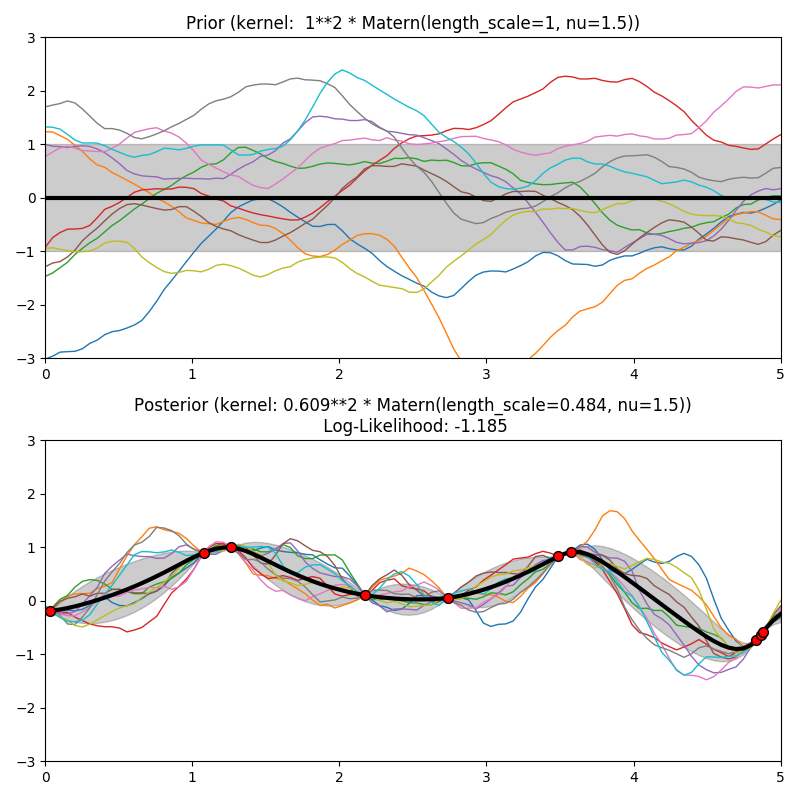
This example illustrates the prior and posterior of a GPR with different kernels. Mean, standard deviation, and 10 samples are shown for both prior and posterior.
Out:
/Users/thomasfan/Documents/scikit-learn-bootstrap/sklearn/gaussian_process/gpr.py:348: UserWarning: Predicted variances smaller than 0. Setting those variances to 0.
warnings.warn("Predicted variances smaller than 0. "
/Users/thomasfan/Documents/scikit-learn-bootstrap/sklearn/gaussian_process/gpr.py:478: ConvergenceWarning: lbfgs failed to converge (status=2): b'ABNORMAL_TERMINATION_IN_LNSRCH'. Increase the number of iterations.
_check_optimize_result("lbfgs", opt_res)
/Users/thomasfan/Documents/scikit-learn-bootstrap/sklearn/gaussian_process/gpr.py:348: UserWarning: Predicted variances smaller than 0. Setting those variances to 0.
warnings.warn("Predicted variances smaller than 0. "
print(__doc__)
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import (RBF, Matern, RationalQuadratic,
ExpSineSquared, DotProduct,
ConstantKernel)
kernels = [1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0)),
1.0 * RationalQuadratic(length_scale=1.0, alpha=0.1),
1.0 * ExpSineSquared(length_scale=1.0, periodicity=3.0,
length_scale_bounds=(0.1, 10.0),
periodicity_bounds=(1.0, 10.0)),
ConstantKernel(0.1, (0.01, 10.0))
* (DotProduct(sigma_0=1.0, sigma_0_bounds=(0.1, 10.0)) ** 2),
1.0 * Matern(length_scale=1.0, length_scale_bounds=(1e-1, 10.0),
nu=1.5)]
for kernel in kernels:
# Specify Gaussian Process
gp = GaussianProcessRegressor(kernel=kernel)
# Plot prior
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
X_ = np.linspace(0, 5, 100)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 10)
plt.plot(X_, y_samples, lw=1)
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("Prior (kernel: %s)" % kernel, fontsize=12)
# Generate data and fit GP
rng = np.random.RandomState(4)
X = rng.uniform(0, 5, 10)[:, np.newaxis]
y = np.sin((X[:, 0] - 2.5) ** 2)
gp.fit(X, y)
# Plot posterior
plt.subplot(2, 1, 2)
X_ = np.linspace(0, 5, 100)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 10)
plt.plot(X_, y_samples, lw=1)
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("Posterior (kernel: %s)\n Log-Likelihood: %.3f"
% (gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)),
fontsize=12)
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 1.383 seconds)